Základem všech učení, která znají svět, je matematika. Přesná vědecká použití formalizovaný jazyk a studuje pořadí, strukturu a vztahy na vybraných abstraktních objektech. Ne všichni studenti mají rádi matematiku složitost a zmatek, ale pravděpodobně proto nedorozumění. Trvalé změny ve vztahu k matematice budou vyžadovat obětavost, soustředění, důslednost, dokonce tvrdohlavost a hlavně praktická řešení. Ve studii je důležité krok za krokem pochopit zpočátku jednoduchý a postupně přejít ke složitějšímu, aniž by zůstalo něco nepochopitelné a špatně koncipované.
Existuje mnoho různých oborů matematiky, které byly dostatečně prozkoumány a objevily se nedávno. Dále jsou popsány základy matematické analýzy - základní počáteční pojmy, definice a pravidla pro studium jednoduchých funkcí jedné proměnné, derivace a diferenciace..
Mezi studenty základních škol došlo k aforismu: „Matematika se stává opravdu komplikovanou, když z ní čísla zmizí.“ Ve skutečnosti se blíží k porozumění některým definicím a zákonům matematické vědy tím, že rozhodují o pravidlech pomocí konkrétních příkladů..
Definice klíčů
Začněme terminologií - jednoduchými obecnými sémantickými významy primárních definic:
- Proměnná - hodnota nebo symbol, může mít libovolnou z mnoha hodnot v
konkrétní oblast (hmotnost nebo výška dítěte)
- Funkce - účel, práce, aktivita, konkrétní akce na proměnné, označíme f (x) (závislost hmotnosti dítěte na jeho výšce)
- Limit - limit, hranice, hrana (horizont - zorné pole)
- Derivát - formovaný, sekundární, plynoucí z jiného, označujeme f '(x) (rychlost při pohybu)
- Diferenciál - rozdíl, rozlišení, oddělení.
Funkce je spravedlivá
Funkce je výsledkem toho, co dělá s proměnnou, která je výsledek výpočtu. Jedná se o vztah prvků, ve kterých změna jedné proměnné způsobí změnu jiné. Rozdělte f (x) na jednoduché a složité.
K zobrazení závislostí se používají následující metody: algebraický, grafický, tabulkový, logický a dokonce i software.
Numerické závislosti se určují algebraicky pomocí symbolů proměnných, rovnic a nerovností (≤ a>), konstruuje se rovnice tvaru: y = f (x), zde x je proměnná nebo argument a y nebo f (x) je funkce. Pro každou konkrétní hodnotu proměnné x z přípustné domény definice odpovídá určitá hodnota y pro danou f (x).
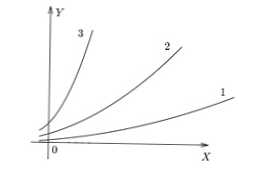
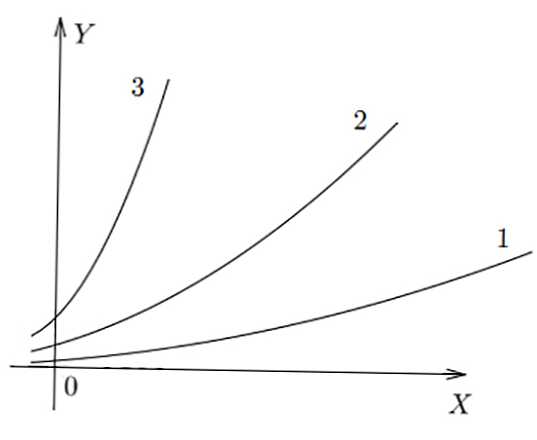
Následující obrázek ukazuje jednoduché grafy 3 různých poměrů. Je vidět, že v f (x) 3 je největší hodnota y získána pro x specifická, v f (x) 1 - nejmenší.
Funkce
Rozlišují se následující elementární výrazy: lineární (přímý), kvadratický (parabola), krychlový, hyperbola, exponenciální, logaritmický, trigonometrický (viz tabulka níže).
Pro analýzu každého typu f (x) se stanoví jejich vlastní vlastnosti (jsou uvedeny níže), pro tento účel se používají pojmy derivace a diferenciálu.
Derivační funkce
Derivát - operátor, který pro originál f (x) podle zákonů o diferenciaci přidružuje další funkci, v určitém bodě charakterizuje změnu v primárním f (x) argumentu x. Pro jeho podrobné pochopení je třeba se zabývat složitějšími definicemi limitu závislosti a diferenciace..
Limit - tato definice je dynamická. Výraz, který x inklinuje k n, se chápe následovně: x získává hodnoty, které jsou blízké n a liší se malým množstvím.
Diferenciál - malá změna nějaké velikosti. Přírůstek se nazývá delta.
Derivát pro f (x) v bodě je limit dělení delty funkce deltou proměnné v daném bodě, pokud má tendence k 0.
Charakteristiku rychlosti změny závislosti v daném bodě, geometricky ji lze znázornit jako hodnotu tan úhlu sklonu alfa tangens k funkci.
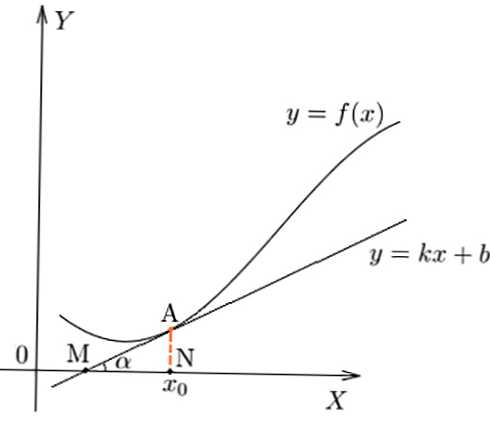
Derivát
Závislost se nazývá diferencovatelná, pokud je definována f '(x). Nalezení derivátu se nazývá diferenciace. Pravidla pro výpočet f '(x) a shody f' (x) ze elementárního f (x) jsou uvedena v následující tabulce
Odvozená funkce také funguje
Každá závislost má určité vlastnosti, jejich poznání a zkoumání můžete analyzovat povahu stavu a změny f (x).
Hlavní vlastnosti:
- Definice a hodnoty mezer v hodnotě.
- Nula f (x)
- Funkce se v některých intervalech zvyšuje nebo snižuje.
- Funkce MAX a MIN, existuje inflexe.
- Sudý nebo lichý f (x)
- Omezená a neomezená funkce.
- Existují nějaké asymptoty.
- Frekvence f (x).

Funkce a deriváty
Při určování charakteristik závislosti pomocí derivace se používají propojení vlastností f '(x) s vlastnostmi f (x) a naopak. Charakteristiky f '(x) lze snadno určit na grafu funkcí a naopak charakteristiky primárního f (x) jsou pochopitelné z grafu f' (x). Stanovení podstaty každé funkce funkce, prozkoumání a vytvoření řetězce vztahů. K určení asymptot v grafech se používá pojem limitů..
Níže jsou uvedeny některé charakteristiky a závislosti f '(x) na f (x):
- Jak f (x) se zvětšuje v intervalu, f '(x) je pozitivní.
- Pokud f (x) klesne v intervalu, f '(x) je záporné.
- V přítomnosti f (x) nemusí být stanoven bod MAX, f '(x) = 0 a tg tečného úhlu změní znaménko z + na -.
- V přítomnosti f (x) nemusí být stanoven bod MIN, f '(x) = 0 a tg úhlu dotyčnice se mění z - na +.
- Při ohýbání f (x) v E se hodnota f '(x) v bodě nezměnila, f' (x) = 0.
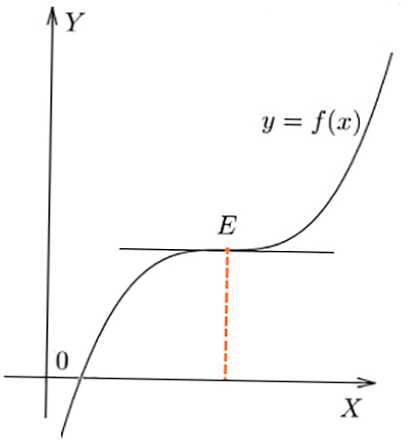
Sklon v bodě E funkčního grafu
Pro výzkum f (x) tvoří schéma, ve kterém je každý krok konstruován podle specifického algoritmu pro výpočet a analýzu vztahů prvků prvků.
Rozdíly ve funkcích a derivátech
Pravidla sčítání a odčítání f (x) jsou stejná jako pravidla těchto akcí během diferenciace. Pravidla pro nalezení f '(x) při akcích multiplikace a dělení funkcí se však liší (jako v tabulce).
Funkce je primární a derivát je sekundární matematická operace, ve většině případů mají odlišné vlastnosti.
Inflexní bod spojité závislosti je nalezen jeho druhou derivací, jeho znaménko by se mělo měnit v oblasti bodu x0.
Existují takové typy funkcí, které nemají f '(x) v bodě x0 (diskontinuální). Ve výrazu ln (| x | -1) derivát není definován v bodě x0 = 1.
Existují výrazy "modulo" podobné y = | x |, které má zalomení v x0.
Pro takové závislosti se používají jen částečně (v intervalech definiční domény) metody studia jejich vlastností pomocí derivátů a není vždy možné přejít z vlastností f '(x) na vlastnosti primární.
Nikde se neobejde bez výjimek z pravidel, dokonce ani v matematice. Aby bylo možné analyzovat a konsolidovat prezentovaný materiál, je nezbytné řešit příklady, praxi, získat zkušenosti s limity, diferenciály a deriváty a směle přejít na integrály..











